儌儞僥傿丒儂乕儖栤戣丂IMD僷僘儖儔儞僪 |
|
| 丂 丂偙偺栤戣偼悢妛幰傕娫堘偊傞傎偳姩堘偄偟傗偡偄忦審晅偒妋棪偺栤戣偩偲偟偰條乆側僒僀僩傗杮偱夝愢偝傟偰偄傑偡丅姩堘偄偟偨悢妛幰偺拞偵偼悢榑傗妋棪榑偱柤崅偄億乕儖丒僄儖僨僔儏傕偄傑偟偨丅偟偐偟丄斵傜偼姩堘偄偼偟偨偑丄妋棪偺峫偊曽傪娫堘偭偨傢偗偱偼側偔丄栤戣偑惓偟偔揱傢偭偰側偐偭偨偩偗偺傛偆偵巚偊傑偡丅 丂忦審晅偒妋棪偲偄偆偺偼崅峑悢妛偱搊応偡傞奣擮偱偡偑丄懡偔偺僒僀僩偱偼丄妋棪偵撻愼傒偺側偄撉幰傕憐掕偟偰偄傞偨傔偐丄忦審晅偒妋棪偺岞幃傪巊偆偺偱偼側偔丄昞側偳傪巊偭偰條乆側夝愢偑側偝傟偰偄傑偡丅偙偺栤戣偼壢妛嶨帍僯儏乕僩儞僾儗僗偱傕庢傝忋偘傜傟丄擇廳偺墌傪昤偒丄撪晹傪暘妱偟偨墌僌儔僼傪俁偮昤偄偰愢柧偟偰偁傝傑偟偨丅 丂偙偙偱偼丄昞傗恾偼巊傢偢丄忢幆偱棟夝偱偒傞榑棟揑側夝朄傪帵偟傑偡偑丄偦偺慜偵偙偺栤戣偵偮偄偰偺攚宨傗栤戣撪梕偍傛傃僱僢僩忋偵偁傞丄傛偔偁傞娫堘偭偨夝愢傪巜揈偟偰偍偒傑偡丅 仠栤戣偺徻嵶偵偮偄偰 弌揟: 僼儕乕昐壢帠揟亀僂傿僉儁僨傿傾乮Wikipedia乯亁傛傝堷梡 儌儞僥傿丒儂乕儖栤戣偲偼丄妋棪榑偺栤戣偱丄儀僀僘偺掕棟偵偍偗傞帠屻妋棪丄偁傞偄偼庡娤妋棪偺椺戣偺傂偲偮偲側偭偰偄傞丅 仸拲丂帠屻妋棪偲偼忦審晅偒妋棪偺侾庬偱偁傞丅 帪偼1990擭丄儌儞僥傿丒儂乕儖偑巌夛幰傪柋傔傞傾儊儕僇偺僔儑乕斣慻偺拞偱師偺傛偆側僎乕儉偑峴傢傟偨丅 丂僾儗乕儎乕偺慜偵暵傑偭偨3偮偺僪傾偑偁偭偰丄1偮偺僪傾偺屻傠偵偼宨昳偺怴幵偑丄2偮偺僪傾偺屻傠偵偼丄偼偢傟傪堄枴偡傞儎僊偑偄傞丅僾儗乕儎乕偼怴幵偺僪傾傪摉偰傞偲怴幵偑傕傜偊傞丅僾儗乕儎乕偑1偮偺僪傾傪慖戰偟偨屻丄巌夛偺儌儞僥傿偑巆傝偺僪傾偺偆偪儎僊偑偄傞僪傾傪奐偗偰儎僊傪尒偣傞丅 偙偙偱僾儗乕儎乕偼丄嵟弶偵慖傫偩僪傾傪丄巆偭偰偄傞奐偗傜傟偰偄側偄僪傾偵曄峏偟偰傕傛偄偲尵傢傟傞丅 僾儗乕儎乕偼僪傾傪曄峏偡傋偒偩傠偆偐丠
丂僯儏乕僗嶨帍 Parade 偵偰丄儅儕儕儞丒儃僗丒僒償傽儞僩偑楢嵹偡傞僐儔儉乽儅儕儕儞偵偍傑偐偣乿偵偍偄偰忋婰偺撉幰搳峞偵傛傞幙栤偵丄乽惓夝偼亀僪傾傪曄峏偡傞亁偱偁傞丅側偤側傜丄僪傾傪曄峏偟偨応崌偵偼宨昳傪摉偰傞妋棪偑2攞偵側傞偐傜偩乿偲夞摎偟偨丅偡傞偲捈屻偐傜丄乽斵彈偺夝摎偼娫堘偭偰偄傞乿偲偺栺1枩捠偺搳彂偑嶦摓偟丄杮栤戣偼戝媍榑偵敪揥偟偨丅 摎偊傪傔偖偭偰偺憶摦 丂搳彂偵偼丄1000恖嬤偄攷巑崋曐帩幰偐傜偺傕偺傕娷傑傟偰偄偨丅偦偺戝晹暘偼乽僪傾傪曄偊偰傕妋棪偼屲暘屲暘乮2暘偺1乯偱偁傝丄3暘偺2偵偼側傜側偄乿偲偡傞傕偺偱偁偭偨丅僒償傽儞僩偼搳彂傊偺斀榑傪帋傒丄摨擭12寧2擔丄悢捠偺斀榑偺庤巻傪徯夘偟偨丅 丂僕儑乕僕丒儊僀僜儞戝妛丂儘僶乕僩丒僒僢僠僗攷巑乽僾儘偺悢妛幰偲偟偰丄堦斒戝廜偺悢妛揑抦幆偺掅偝傪桱椂偡傞丅帺傜偺娫堘偄傪擣傔傞帠偱尰忬偑夵慞偝傟傑偡乿 丂僼儘儕僟戝妛丂僗僐僢僩丒僗儈僗攷巑乽孨偼柧傜偐側僿儅傪偟偨乮拞棯乯悽奅嵟崅偺抦擻巜悢曐桳幰帺傜偑悢妛揑柍抦傪偙傟埲忋悽娫偵峀傔傞嬸峴傪捈偪偵巭傔丄抪傪抦傞傛偆偵両乿 丂僒償傽儞僩偼丄傛傝娙堈偵偟偨昞傪宖嵹乽僪傾傪曄偊傟偽彑偰傞偺偼3夞偺撪2夞丄晧偗傞偺偼3夞偺撪1夞偩偗丄偟偐偟僪傾傪曄偊側偗傟偽彑偰傞偺偼3夞偺撪1夞偩偗乿偲弎傋傞丅偙偺栤戣偵娭偡傞1991擭2寧17擔晅丄3夞栚偺婰帠偺抜奒偱僒償傽儞僩偵懳偡傞斀榑偼9妱掱搙傪愯傔傞丅 丂乽尰幚偑捈娤偲斀偡傞帪丄恖乆偼摦梙偡傞乿偲僒償傽儞僩偼僐儔儉偱斀榑偺惡偵墳偠丄壓婰偺愢柧傪帋傒傞丅 丂乽 巌夛幰偑僪傾傪奐偗偰傒偣偨捈屻偵UFO偑僗僥乕僕偵摓拝偟偰塅拡恖偑弌偰偒偨偲壖掕偡傞丅恖娫偺弌応幰偑嵟弶偵慖傫偩斷傪塅拡恖偼抦傜偢偵巌夛幰偑傑偩奐偗傜傟偰偄側偄2偮偺斷偺偳偪傜偐傪慖戰偡傞傛偆塅拡恖偵姪傔傞偲丄偙偺帪偺妋棪偑屲暘屲暘偵側傞丅偟偐偟丄偦傟偼塅拡恖偑杮棃偺弌応幰偑巌夛幰偐傜摼偨僸儞僩傪抦傜側偄偨傔偱偁傞丅壖偵宨昳偑斷2偵偁傞応崌巌夛幰偼斷3傪奐偗傞丅斷3偵宨昳偑偁傞応崌偼斷2傪奐偗傞丅偮傑傝宨昳偑斷2傑偨偼斷3偵偁傞側傜丄弌応幰偑斷偺慖戰傪曄偊傟偽彑棙偡傞丅亀偳偪傜偐偱傕彑偰傞偺偱偡両亁偱傕斷傪曄偊側偗傟偽丄斷1偵徿昳偑偁傞応崌偟偐彑偰側偄偺偱偡丅 乿 丂僒償傽儞僩偺嵞嵞乆夝愢偱傕戝榑憟傊偲敪揥丄乽斵彈偙偦娫堘偭偰偄傞乿偲偄偆姶忣揑側僕僃儞僟乕栤戣偵傑偱旘傃壩偟偨丅 ---堷梡廔傢傝 丂埲壓徣棯 丂 埲忋偺傛偆偵丄愱栧壠傕岎偊偰媍榑偵側偭偨傢偗偱偡偑丄偦偺尨場偼忋弎偺惵帤偱彂偄偰偁傞僎乕儉偺撪梕偵偮偄偰岆夝偑偁偭偨偐傜偱偁傠偆偲巚傢傟傞丅僒償傽儞僩偼悢妛幰偵懳偟偰偼丄埲壓偺傛偆偵尵偊偽壗偱傕側偐偭偨偺偱偼偁傞傑偄偐丅 丂乽偙偺僎乕儉偱偼丄巌夛幰偼偳傟偑摉偨傝偱偁傞偐傪抦偭偰偄偰丄斵偼昁偢丄偼偢傟偺僪傾傪奐偗偰尒偣傑偡乿 丂僒償傽儞僩偺愢柧傪傛偔撉傔偽丄忋婰偺忦審偑慜採偱偁傞偙偲偵婥偯偔偼偢偱偡偑丄偍偦傜偔嵟弶偺姩堘偄偐傜敳偗弌偣側偐偭偨偺偱偟傚偆丅 丂忋偺傛偆側帠幚傪彸抦偺忋偱偙偺栤戣傪峫偊傟偽丄僒償傽儞僩偺夝愢傕暘偐傝傗偡偄偲巚傢傟傞偑丄僎乕儉偺徻嵶偑偡傋偰柧傜偐偵側偭偨尰嵼偱傕丄昞傪梡偄偰柺搢側夝愢偑偟偰偁傝傑偡丅偙傟偼丄巌夛幰偑侾偮偺僪傾傪奐偗偨屻偼巆偭偨俀偮偺偆偪侾偮偑摉偨傝偩偐傜丄摉偨傞妋棪偼俀暘偺侾偲偄偆峫偊偵榝傢偝傟傗偡偄偲偄偆偙偲偱偟傚偆丅 丂幚嵺丄巌夛幰偑偳傟偑摉偨傝偱偁傞偐傪抦傜側偄応崌丄俛偐俠傪奐偗偰偼偢傟偱偁偭偰傕丄師偺傛偆側係偲偍傝偺忬嫷偑峫偊傜傟丄偄偢傟偺忬嫷傕弌尰妋棪偑摨偠偱偡偐傜僪傾傪曄偊偰傕曄偊側偔偰傕摉偨傞妋棪偼俀暘偺侾偵側傝傑偡丅 仸壓婰係偲偍傝偑摨偠弌尰妋棪偱偁傞棟桼偼屻偱愢柧偟傑偡丅 恾嘥
丂丂 丂偙偺栤戣偼丄栤戣偺堄枴偑惓偟偔揱傢偭偰傕懡偔偺恖偵棟夝偟偯傜偔姶偠傜傟傞傛偆偱丄僱僢僩偱忋埵偵偁傞夝愢偱傕岆偭偨傕偺偑偁傝傑偡丅 丂埲慜丄乽儌儞僥傿儂乕儖栤戣乿偱YouTube偱専嶕偟偰傒傞偲崟斅偵昞傪彂偄偰夝愢偟偰偁傞傕偺偑嵟忋埵偵偁傝傑偟偨丅戝妛庴尡惗傑偱傪懳徾偵偟偨偁傞弇偺夝愢偱丄旕忢偵暘偐傝傗偡偄偲偄偆昡敾偺傛偆偱偡偑丄戝偒側娫堘偄偑俀偮偁傝丄俀偮偁傞偨傔偵偨傑偨傑摎偑崌偭偰偄傞傢偗偱偡偑丄偦傟傪僐儊儞僩棑偱巜揈偟偰傕旑鎺拞彎偲傒側偝傟偨偺偐丄僐儊儞僩偼嶍彍偝傟丄摦夋偼枹偩偵宖嵹偝傟偰偄傑偡丅2020擭5寧尰嵼偼俁斣栚偁偨傝偺偲偙傠偵昞帵偝傟偰偄傞傛偆偱偡偑丄嵞惗夞悢偼夝愢偺摦夋偲偟偰偼嵟傕懡偄傛偆偱偡丅丂懡偔偺恖偑偙傟傪尒偰暘偐偭偨婥偵側傞偺偼儌儞僟僀偑偁傝傑偡偺偱丄崱夞偼幚嵺偺塮憸傪婎偵偟偨夋憸傪堷梡偟偰娫堘偄傪暘偐傝傗偡偔巜揈偟偰偍偒傑偟偨丅埲慜偼崟斅偺夝愢恾偲摨偠柾幃恾傪巊偭偰丄偳偺摦夋傪懳徾偵偟偨傕偺偐暘偐傜側偄傛偆側彂偒曽偵偟偰偄傑偟偨偑丄嬐偐俀乣俁擭偺娫偵丄偺傋係枩恖偑偙偺娫堘偭偨夝愢傪尒偰偄傞忬嫷傪峫偊丄幚嵺偺摦夋偵偁傞崟斅偺恾傪梡偄偰娫堘偄傪巜揈偟傑偟偨丅傆偮偆偵夝愢偡傞傛傝傕偙偺栤戣偺杮幙偑暘偐傞夝愢偵側傝傑偟偨偺偱丄偦偺揰偱偼椙偄尒杮偵側偭偨偲巚偄傑偡丅YouTube偺摦夋偼搳峞幰偑偄偢傟丄娫堘偄偵婥偯偄偰嶍彍偡傞偙偲偵側傞偲巚偄傑偡丅 仸挊嶌尃忋偼斸敾傗娫堘偄偺巜揈傪偡傞応崌偺堷梡偼擣傔傜傟偰偍傝丄堷梡偵嵺偟偰偼弌揟尦傪柧帵偡傞偙偲偑姷椺偲側偭偰偄傑偡偑丄愭曽偺棫応傕偁傝傑偡偺偱柤徧偺婰嵹偼抳偟傑偣傫丅乮偙傟偼傛偔偁傞揟宆揑側娫堘偄偱偁傝丄懠偺僒僀僩偱傕偙偺傛偆側娫堘偄傪尒庴偗傑偡乯 2021擭11寧5擔捛婰 ********************************************* 偙偺儁乕僕偼IMD僷僘儖儔儞僪偵宖嵹偟偰偄傑偟偨偑丄忋婰YouTube偺摦夋偺僐儊儞僩棑偵娫堘偄偱偁傞偙偲傪巜揈偟丄夝愢儁乕僕偺儕儞僋愭傪帵偟偨偲偙傠丄偦偺僐儊儞僩偑嶍彍偝傟丄乽悢妛僷僘儖乿偺僉乕儚乕僪偱専嶕偡傞偲忋埵偵昞帵偝傟偰偄偨IMD僷僘儖儔儞僪偺僒僀僩偦偺傕偺偑専嶕懳徾偐傜枙徚偝傟偰偟傑偄傑偟偨丅Google偲偦偺専嶕僄儞僕儞傪巊偭偰偄傞Yahoo,偦偟偰,嵟忋埵儁乕僕偵宖嵹偟偰偄偨MSN乮儅僀僋儘僜僼僩偺専嶕僄儞僕儞乯偐傜傕嶍彍偝傟傑偟偨丅嵟屻傑偱挷傋偰傕宖嵹偝傟偰偍傝傑偣傫丅偍偦傜偔丄Youtube偺摦夋偺嶌惉幰傑偨偼偦偺娭學幰偑挊嶌尃怤奞偱偁傞偲偟偰慽偊偨傕偺偲悇應偟偰偄傑偡丅娫堘偭偨夝愢偑懡偔偺恖偵徯夘偝傟丄偦偺娫堘偄傪巜揈偟丄慡偔怴偟偄敪憐偱惓偟偄夝愢傪偟偨儁乕僕偑恖偺栚偵怗傟偵偔偄傛偆側忬嫷偑弌尰偟偰偄傑偡丅尰戙偺僱僢僩幮夛偺偁傝曽傪峫偊傞忋偱丄旕忢偵嶲峫偵側傞尰徾偲峫偊偰偄傑偡丅 ********************************************* 偦偺屻丄Google偲MSN偺専嶕僄儞僕儞偱丄悢偐寧娫偼埲慜偺傛偆偵暅妶偟偰偄傑偟偨偑丄尰嵼偼姰慡偵幷抐偝傟偰偼偄傑偣傫偑丄埲慜偲偼戝堘偄偱偡丅 仸偙偺摦夋偺僐儊儞僩棑傪尒偰傒傞偲娫堘偄偵婥偯偄偰偄傞恖傕偄傞傛偆偱丄嬶懱揑偵師偺傛偆側搳峞偑偁傝傑偡丅 椺丂 ************************* 寬擇偝傫 帺暘偑惓夝偟偰偄傞応崌丄憡庤偼懠偺俀枃傪奐偗傞僷僞乕儞偑懚嵼偟偰偍傝丄偦偺揰偑寚棊偟偰傑偣傫偐丅偦偺応崌丄2彑2攕偲側傝丄妋棪偼摨摍偵側傝傑偡丅傛偭偰丄偙偺愢柧偩偲慖戰巿傪曄偊偰傕曄偊側偔偰傕摨偠偵側傞偲巚偄傑偡丅傕偭偲暘偐傝傗偡偔愢柧偟偰梸偟偄丅 ************************* 乽暘偐傝偵偔偄愢柧乿偲偄偆偺偱偼側偔丄崻杮揑偵岆傝偱偡丅 ------捛婰廔傢傝 堷梡恾
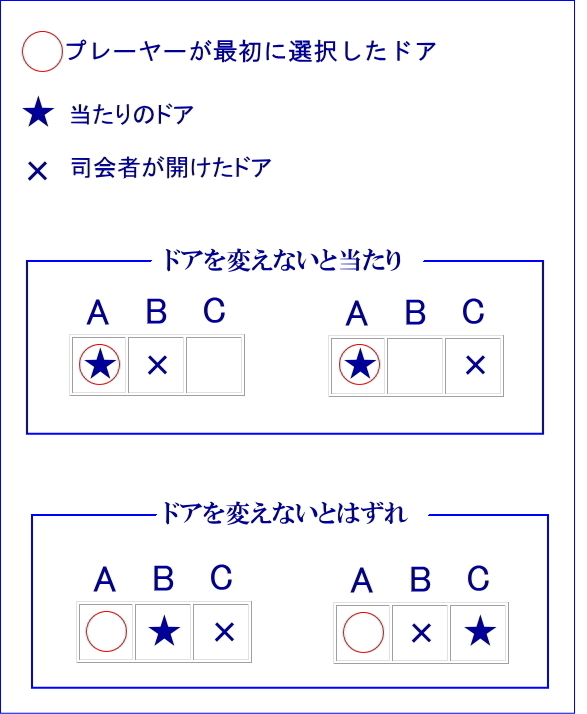
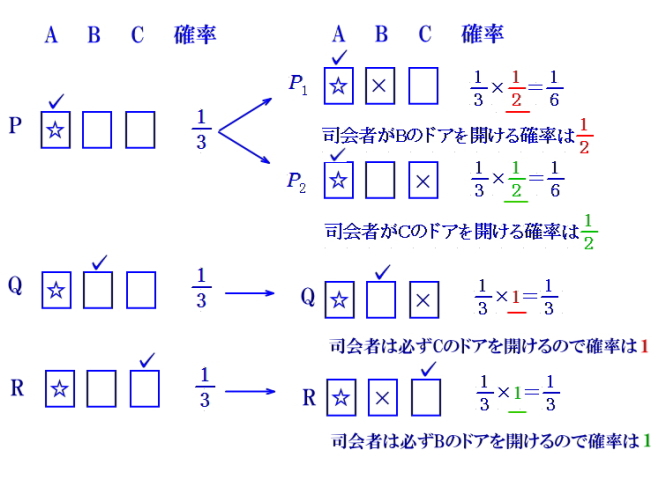
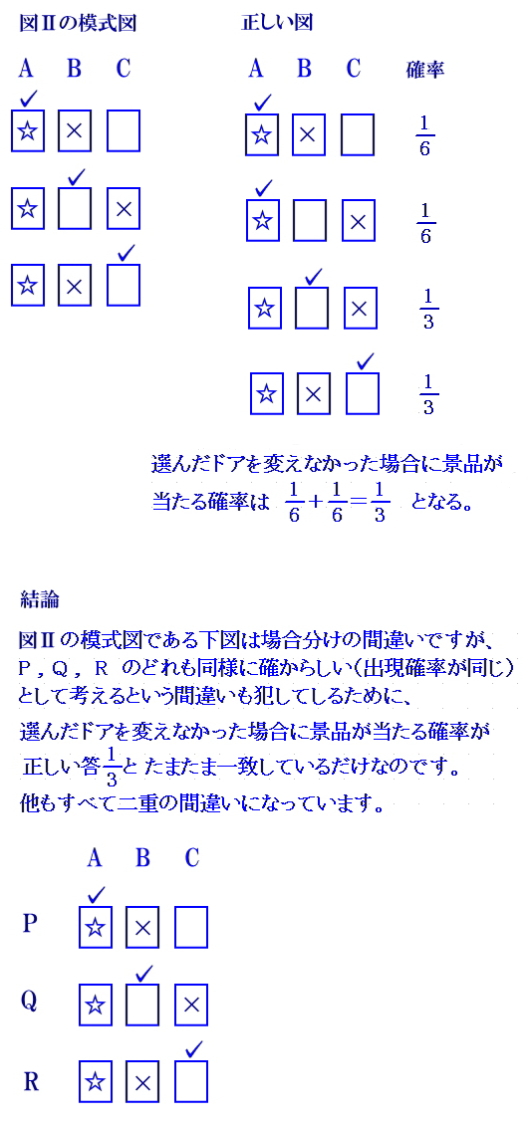
丂忋偺夝愢偼嵟弶偐傜娫堘偄偱偡丅 丂堦斣嵍偺, A偵宨昳偑偁傞応崌傪椺偵偲偭偰夝愢偟傑偡丅 丂摦夋偱偼仚偑宨昳丄僠僃僢僋 恾嘦  丂昞偵妋棪偑彂偒崬傑傟偰偄側偄偙偺傛偆側恾偼丄偳傟傕摨條偵妋偐傜偟偄乮摨偠妋棪偱婲偒傞乯帠徾傪偡傋偰楍嫇偟偰妋棪傪媮傔傞偲偒偵巊偆傕偺偱偁傝丄撉幰傕偦傟偼暘偭偰偄傞偲巚偄傑偡偑丄巌夛幰偑偳傟偑摉偨傝偺僪傾偱偁傞偐傪抦偭偰偄偨側傜丄偙傟傜偼摨條偵妋偐傜偟偄乮摨偠弌尰妋棪乯偲偼尵偊傑偣傫丅偙傟偑戞侾偺娫堘偄偱偡丅丂巌夛幰偑傑偩僪傾傪奐偗偰偄側偄忬懺偼壓恾偵側傝丄偙傟傜P, Q, R偺俁僷僞乕儞偼摨偠妋棪偱弌尰偟傑偡丅偮傑傝丄宨昳偑A偺僪傾偵偁傞応崌偺P, Q, R偺妋棪偼丄偄偢傟傕俁暘偺侾偵側傝傑偡丅 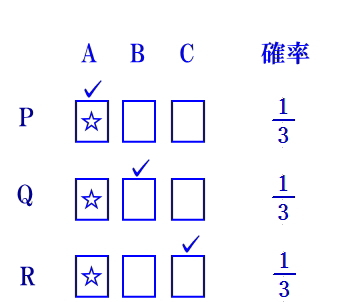 丂偙偙偱巌夛幰偼宨昳偺偁傞僪傾偲僾儗乕儎乕偑慖傫偩僪傾埲奜偐傜侾偮偺僪傾傪慖傃丄偦偺僪傾傪奐偗傑偡丅 壓恾偺嵍懁偼巌夛幰偑僪傾傪奐偗傞慜丄塃懁偼僪傾傪奐偗偨屻偱偁傝丄亊偼巌夛幰偑奐偗偨僪傾偱偡丅
丂忋婰夝愢偱柧傜偐側傛偆偵, 崟斅偺嵟傕嵍偺晹暘偱偁傞恾嘦偺柾幃恾偼壓偺嵍恾偲側傝傑偡偑丄惓偟偄恾偼塃恾偲側傝傑偡丅
丂巌夛幰偑僪傾偺拞恎傪抦傜偢偵丄偨傑偨傑奐偗偨僪傾偑偼偢傟偱偁偭偨応崌偼丄僾儗乕儎乕偑嵟弶偵慖傫偩僪傾傕丄傕偆堦偮偺奐偗傜傟偰偄側偄僪傾傕摉偨傞妋棪偼俀暘偺侾偱偁傞偑丄巌夛幰偑丄偼偢傟偺僪傾偩偲暘偐偭偰偄偰丄偼偢傟偺僪傾傪奐偗傞偙偲偵側偭偰偄偨偲偄偆偙偲側傜丄嵟弶偵慖傫偩僪傾偑摉偨傞妋棪偼俁暘偺侾丄傕偆堦偮偺奐偗傜傟偰偄側偄僪傾偺摉偨傞妋棪偼俁暘偺俀偲側傝傑偡丅 丂巌夛幰偑抦偭偰偄偨偐丄抦傜側偐偭偨偐丄偦傟偑廳戝側億僀儞僩偱偁傝丄惓偟偄夝朄偼丄乽抦偭偰偄偰丄昁偢偼偢傟偺僪傾傪奐偗傞乿偲偄偆慜採忦審偑斀塮偝傟偨傕偺偵側傝傑偡丅 丂偟偐偟丄偙偺栤戣乮僎乕儉乯偼尦乆丄妋棪偵撻愼傒偺側偄堦斒偺恖偨偪傪懳徾偵偟偨傕偺偱偟偨偐傜丄偱偒傞偙偲側傜丄妋棪偺峫偊曽傪傎偲傫偳抦傜側偄恖偱傕娙扨偵棟夝偱偒傞傛偆側忢幆偱暘偐傞夝朄偑朷傑偟偄偲巚偄丄師偺傛偆側夝朄傪峫偊傑偟偨丅偙偺儁乕僕傪彂偄偰偄傞尰抜奒偱偼丄僱僢僩忋偱傕壓婰偺傛偆側峫偊曽偼尒摉偨傝傑偣傫偑丄偄偢傟丄偙偺傛偆側峫偊曽偑峴偒搉傝丄偙偺堦晽曄傢偭偨峫偊曽偑傆偮偆偺夝愢偺傛偆偵姶偠傜傟傞傛偆偵側傞偐傕偟傟傑偣傫丅偙偺傛偆側峫偊曽偼丄怓乆側僶儕僄乕僔儑儞偑峫偊傜傟傑偡偑丄杮幙偼摨偠偱偡丅婔偲偍傝偐偺応崌暘偗傪峫偊偨偲偒偼丄偦傟傜偑摨條偵妋偐傜偟偄乮弌尰妋棪偑摨偠乯偲偄偆偙偲傪徹柧偟偨傝丄捈姶偵棅偭偨傝偡傞昁梫偑偁傝傑偡偑丄偙偺峫偊曽偺棙揰偼丄偦偺昁梫偑側偔丄忢幆偱敾抐偱偒傞偙偲偱偡丅 忢幆偱棟夝偱偒傞榑棟揑側夝朄 偙偺栤戣偺慜採忦審傪傕偆堦搙妋擣偟偰偍偒傑偡丅 僾儗乕儎乕偑侾偮偺僪傾傪慖傫偩偲偒丄偦傟偑摉偨傝偱偁傞妋棪偼俁暘偺侾偱偁傞丅僾儗乕儎乕偼俙丆俛丆俠偺僪傾偺偆偪俙傪慖傫偩丅廬偭偰丄俛偐俠偺彮側偔偲傕堦曽偑偼偢傟偱偁傞丅丂巌夛幰偼偳傟偑摉偨傝偺僪傾偐傪抦偭偰偍傝丄昁偢偼偢傟偺僪傾傪奐偗傞丅 亙夝摎侾亜 丂丂 偙偺栤戣偱偼僾儗乕儎乕偑侾恖偄偰丄俙丄俛丄俠偺僪傾偺偆偪侾偮傪慖傫偩偲偄偆偙偲偵側偭偰偄傞偑丄忬嫷傪彮偟曄偊丄僾儗乕儎乕偼俹偝傫偲俻偝傫偺俀恖偑偄偰丄嵟弶偵俹偝傫偑僪傾俙傪慖傫偩偲偟傑偟傚偆丅俻偝傫偼拪慖偱摿暿僎僗僩偵慖偽傟偨恖偱偟偨偺偱丄巆傝偺僪傾俛偲僪傾俠偺椉曽傪奐偗偰丄偳偪傜偐偵宨昳偑擖偭偰偄偨傜偦傟傪栣偊傞偙偲偵側傝傑偟偨丅偡傞偲俹偝傫偑摉偨傞妋棪偼俁暘偺侾偱偁傞偑丄俻偝傫偑摉偨傞妋棪偼俁暘偺俀偱偡丅斣慻傪惙傝忋偘傞偨傔偵俹偝傫偲俻偝傫偼摨帪偵僪傾傪奐偗傞偙偲偵側傝傑偟偨丅偟偐偟丄僪傾偲僪傾偑棧傟偰偄傞偨傔偵丄俻偝傫偼摨帪偵俀偮偺僪傾傪奐偗傞偙偲偑偱偒傑偣傫丅偦偙偱丄偡傋偰偺僪傾偺拞恎傪抦偭偰偄傞巌夛幰偑丄乽僪傾俠偼丄偼偢傟偩偐傜俠偼奐偗傞昁梫偼偁傝傑偣傫乿偲崘偘傑偟偨丅摉慠偱偡偑丄巌夛幰偑偦偺傛偆偵崘偘偰傕丄俻偝傫偺摉偨傞妋棪偑俁暘偺俀偐傜俀暘偺侾偵尭偭偨傝偡傞偼偢偼偁傝傑偣傫丅壗屘側傜丄B偐C偺彮側偔偲傕堦曽偑偼偢傟偱偁傞偺偼摉偨傝慜偱偁傝丄偼偢傟偺僪傾傪侾偮抦傜偣偰傕丄偦傟偑B偐C偐偺堘偄偵傛偭偰丄Q偝傫偑摉偨傞妋棪偵堘偄偑弌偰偔傞傢偗偱偼側偄偐傜偱偡丅拞恎傪抦偭偰偄傞巌夛幰偑丄Q偝傫偑奐偗傞庤娫偑徣偗傞傛偆偵丄偼偢傟偺僪傾傪侾偮嫵偊偨偩偗偱偡偐傜丄Q偝傫偑摉偨傞妋棪偼埶慠偲偟偰俁暘偺俀偲偄偆偙偲偵側傝丄僪傾B偑摉偨傞妋棪偑俁暘偺俀偲偄偆偙偲偵側傝傑偡丅廬偭偰丄尦偺栤戣偱峫偊傞偲丄僾儗乕儎乕偑俙偺僪傾傪慖傃丄巌夛幰偑俠偺僪傾傪奐偗偰丄偼偢傟偱偁傞偙偲傪帵偟偨側傜丄俛偺僪傾偑摉偨傞妋棪偼俁暘偺俀偱丄俙偑摉偨傞妋棪偼俁暘偺侾偺傑傑偩偲偄偆偙偲偵側傝傑偡丅 **************************** 暿夝 僪傾偑俆偮偁傞応崌偵暿夝傪峫偊偰傒傑偟傚偆丅 宨昳偼侾偮偺僪傾偺偲偙傠偵偟偐偁傝傑偣傫丅
丂崱夞傕忋婰偲摨偠傛偆偵丄僾儗乕儎乕偼P偝傫偲Q偝傫偺俀恖偱偡偑丄崱搙偼P偝傫偲Q偝傫偼懳摍偱偡丅傑偢P偝傫偑僪傾A傪慖傃傑偟偨丅偦偺屻丄Q偝傫偼巆傝係偮偺僪傾偐傜侾偮傪慖偽側偗傟偽側傝傑偣傫丅Q偝傫偑偳傟傪慖傫偱傕P偝傫偲Q偝傫偺摉偨傞妋棪偼摨偠偱丄俆暘偺侾偱偡丅偦偙偱壗傪峫偊偨偐丄Q偝傫偼偳傟偑摉偨傝偱偁傞偐傪抦偭偰傞巌夛幰偵丄乽B丄C丄D丄E偺偆偪丄彮側偔偲傕俁偮偼偼偢傟偩偐傜丄俁偮偺偼偢傟偺僪傾傪嫵偊偰偔傟乿偲尵偄傑偟偨丅偙偙偱丄乽偦傟傕偦偆偩偹乿偲尵偭偰嫵偊傞巌夛幰偼傑偢偄傑偣傫丅壗屘側傜丄P偝傫偑偼偢傟傞妋棪偼係/俆偱丄P偝傫偑慖傫偩僪傾偑偼偢傟偺僪傾偱偁偭偨側傜丄俁偮偺偼偢傟偺僪傾傪嫵偊傞偲偄偆偙偲偼丄Q偝傫偵摉偨傝偺僪傾傪嫵偊傞偺偲摨偠偙偲偵側傝丄晄暯摍偵側傞偐傜偱偡丅偮傑傝丄俁偮偺偼偢傟偺僪傾傪奐偗偰嫵偊偨傜丄B丄C丄D丄E偺偆偪奐偗傜傟偢偵巆偭偨僪傾偑摉偨傞妋棪偼丄P偝傫偑偼偢傟傞妋棪偲摨偠俆暘偺係偲偄偆偙偲偵側傝傑偡丅偙偺榑棟偼僪傾偑俁偮偺偲偒傕揔梡偱偒傑偡丅 屻婰 丂儌儞僥傿儂乕儖栤戣偼丄偍偦傜偔丄栤戣偺忦審偑惓妋偵揱傢偭偰偄側偐偭偨偨傔偵丄悢妛幰傕姫偒崬傫偩憶偓偵側偭偨偲巚傢傟傑偡偑丄偙傟傛傝擇廫悢擭慜偵榖戣偲側偭偨栤戣偵乽俁廁恖偺栤戣乿偑偁傝傑偡丅偙偺栤戣偼栤戣偑岆夝偝傟傞梋抧偼偁傝傑偣傫偱偟偨偑丄杮幙揑偵偼儌儞僥傿儂乕儖栤戣偲摨偠偱偡丅偟偐偟側偑傜丄栤戣偺愝掕傗昞尰偑岻柇偵偱偒偰偄傞偨傔偵僱僢僩忋偵偁傞夝愢傕暋嶨偵側偭偰偄傑偡丅
|