ある月を30日にするか31日にするかは、１年が365日でありさえすれば大した問題ではないように
	思えるかもしれません。 実際、現在の暦は後述するように古代ローマの皇帝が気まぐれに決めてし
	まったものであるということが文献に記されています。
	ところが、例えば８月と9月の日数を入れ替えたりすると、年月日からその日が何曜日である
	かを求めるための下記のような類の如何なる式も創ることが不可能になります。　 　　　　　　―― Ａ
	つまり、暦は年月日からその日が何曜日であるかを求める式を遠い将来創ることができるように、
	偶然に、しかも綿密につくられたということになります。
	しかもこの式は整然としています。（１,２,３,４,５に注目!)よく調べてみると、これは１週間が７日
	であることも一因であることがわかりますが、この７という数は現代の暦が創られた時代に発見されて
	いた太陽系の星の数に由来しています。偶然！
	、、　が太陽、月、地球、１〜５が火星〜土星（順不同？）と解釈するのもおもしろい。 　―― Ｂ

★	西暦 年 月 日が何曜日であるかを求める方法。（自分の誕生日で計算してみよう）
	の値を求める。ただし［　］の部分は小数点以下を切り捨てる。

	Ｎの値を７で割り、その余りが ０，１，２，３，４，５，６　のとき、 日、月、火、水、木、金、土、となる。 ただし、１月、２月は前年の13月、14月 として計算する。		注 　１年365日と地球の公転周期とのずれを調整するための、うるう年は、近世になって更に正確に定められました。 それは西暦年が100で割り切れて400で割り切れない年はうるう年としないというものです。 従って正確にはこの式に、次の式を加えなければればなりませんが、西暦2000年から100年前後以内であれば関係ありません。 ※カレンダーに合わせるために１を加えました。 ※天王星、海王星、冥王星は近世になって発見さ　れましたが、冥王星の質量は天王星や海王星の　数百分の１で、尚且つ地球からかなり離れてい　るため、地球の自転や公転周期には影響を及ぼさないと考えてよいでしょう。 ※前述Ｂの言い分を通すため、天王星、海王星は、それぞれ上の補正式の -[x/100]と+[x/400]に対応するものと勝手ながら解釈しておきます。(?_?) 　冥王星が太陽系の惑星の仲間にされていたときは最後の＋１を冥王星に対応させていましたが、　＋１はカレンダーに合わせるためのもので、自転や公転周期とは関係ない部分ですから、苦しい辻褄合わせだったのですが、冥王星が惑星からはずされてすっきりしました。 　国際天文学連合（ＩＡＵ）の総会では惑星の数を12個にする案が出されて紛糾しましたが、最終的には８個に決定されました。さすがＩＡＵ！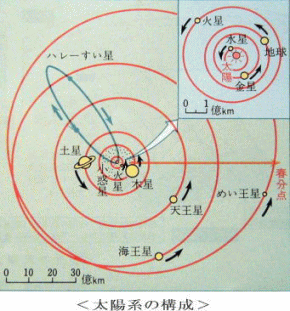
	［問題］カレンダーを基に上の式を導いてください。 ●上式の３／５という数値を容易に見つける方法を発見できれば、上文下線部（Ａ）も納得でき、暦が巧妙に作られていることも分かります。 　あとはそうやって作った式をカレンダーに合わせるために、１か８を加えるのですが、８を加えて、値が整数になるように記号[ 　]を使えば、上式になります。 （図書館などで調べようとしても無駄ですので念のために） 　　　　　現代の暦について 　現代の暦は古代ローマの皇帝アウグストゥスが、それまでのユリウス暦を気まぐれに改定したものであるということが暦の歴史として、概ね以下のように記されています。
	ユリウス暦を見ると、１月から6月までの月名は、ローマにとって重要な神の名前となっている。ところが７月にはアウグストゥスの大叔父カエサル（シーザー）の名前ユリウス(Julius)が付けられている。そこで彼は自分も暦に名を残そうと、トラキア、アクティウムの戦いに勝利をおさめた8月の月名を、戦勝記念という大義名分の下にアウグストゥスと変えてしまった。 　しかも皇帝である自分の月が他の月より日数が少ないのは皇帝の権威にかかわるといって（注参照）、8月を31日に格上げし、その代わりに2月を1日少なくして28日に切り詰めたのである。ところがそうすると、7月、8月9月と、31日の月が3ヶ月続くようになってしまう。そこで7月は大叔父の月なので手をつけない代わりに、9月を30日とし、10月を31日、11月を30日、12月を31日と、1日ずつ増減して、大の月と小の月が交互になるように定めた。 注　古代ローマでは、日数の多い月を大の月、少ない月　　を小の月と呼んだ。
	歴史上の記述は以上のような内容ですが、暦を研究している専門家は、アウグストゥスは改定以前の「奇数月が大の月という整然とした暦」に余計なことをしてしまったと述べている。（ローマでは奇数を尊び、偶数を嫌った） 　しかし、上に示した、年月日から曜日を求める関数式の美しさという観点からは、むしろその方がよかったということになるでしょう。 　奇数と偶数に優劣を認めず、大の月、小の月などの概念も持たない現代から見れば、アウグストゥスの気まぐれは未来を見つめていたと言うべきか。 　しかも大の月が連続することが望ましくないなら、12月が31日なのだから、もともと少ない2月は30日のままにしておいて、1月を30日としそうなものですが、そうはしなかったというのも見事です。 　以上のことは、普通に考えれば、関数式を念頭において改定したのではないかと思えますが、暦の変遷の歴史についての書物には、紀元前３世紀の古代ローマ最初の暦から現代の暦に至るまで、エピソードを交えて、実に細かな経緯が書いてあるにも拘らず、上の関数式と結びつけたものは、今のところ見当たらないようです。
	2000年2月28日　辻