答
	図１		ＡとＢを入れ換えるには横棒が最低１本必要。
	図２		Ａ，Ｂ，Ｃを逆順にするには横棒が最低３本必要。
	図３		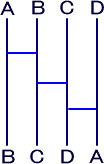Ａ，Ｂ，Ｃ，ＤのＡだけを一番右に移動させるには 最低３本の横棒が必要。
	図４		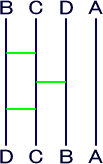図３の下に別のあみだくじを継ぎ足してＢ，Ｃ，Ｄ，Ａの Ｂ，Ｃ，Ｄの部分だけを逆順にするには図２と同じ位置 関係にある３本の横棒を持つ図４に示すあみだくじが あればよい。
	図５		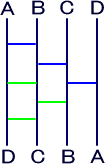図３の下に図４を繋ぎ合わせたものが図５である。
	図６		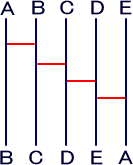Ａ，Ｂ，Ｃ，Ｄ，ＥのＡだけを一番右に移動させるには 最低４本の横棒が必要。
	図７		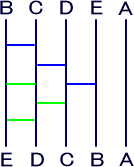図６のＢ，Ｃ，Ｄ，Ｅ，ＡのＢ，Ｃ，Ｄ，Ｅの部分だけを逆順に するには図５と同じ位置関係にある６本の横棒をもつ図７ に示すあみだくじがあればよい。
	図８		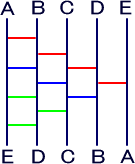図６の下に図７を繋ぎ合わせたものが図８である。
		以上を繰り返して下記のようなあみだくじを作れば、Ａ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆ，Ｇ，Ｈ，Ｉ，Ｊの 10個が全て逆順になる。 このときの横棒の本数は、１＋２＋３＋４＋５＋６＋７＋８＋９＝４５　より４５本
	図９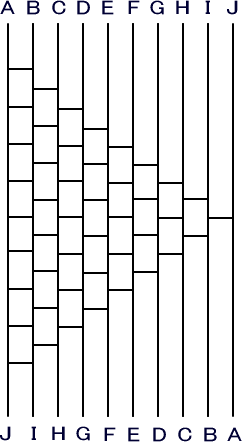
		上記の解法では４５本が最低本数であることの証明にはなっていません。 例えば、Ａ，Ｂ，Ｃ，Ｄを全て逆順にするあみだくじは図５だけではなく、 下記のようなものでも可能であり、横棒の本数は図５と同じ６本です。
	図10
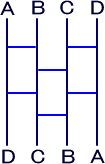		Ａ，Ｂ，Ｃ，Ｄを逆順にするためには横棒が最低６本必要である理由は 次のように説明できます。
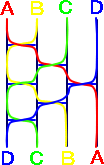
		まず、図５に示したあみだくじのそれぞれの経路を、なめらかな線で 書くと次のようになります。
	図11
		↓
	図12		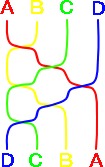図11のなめらかな線の部分だけを抜き出したものが左図 になります。
		↓
	図13		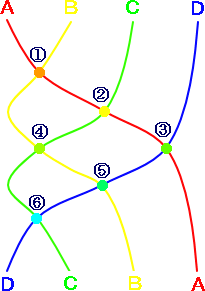左図は図12の線を更になめらかにしたもので、あみだくじの 横棒１本が、線と線の１つの交点に対応しています。 横棒のところでは図１で示したように、左右の入れ替え が起こりますので、交点でも左右が入れ替わります。 Ａ，Ｂ，Ｃ，Ｄを逆順にするためには、 ＡとＢの入れ替え　Ａ⇔Ｂ　�@ ＡとＣの入れ替え　Ａ⇔Ｃ　�A ＡとＤの入れ替え　Ａ⇔Ｄ　�B ＢとＣの入れ替え　Ｂ⇔Ｃ　�C ＢとＤの入れ替え　Ｂ⇔Ｄ　�D ＣとＤの入れ替え　Ｃ⇔Ｄ　�E が必要ですから、少なくとも６個の交点が必要です。 つまり、横棒は少なくとも６本必要になります。 ※異なる色の線が１度だけ交わる場合が、横棒を 　 最低本数にしたあみだくじに対応します。
		Ａ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆ，Ｇ，Ｈ，Ｉ，Ｊ の10個を逆順にするためには以下の入れ替えが必要になります。
		従って、少なくとも必要な横棒の本数は 1＋2＋3＋4＋5＋6＋7＋8＋9＝45　より　45本
		ＩＭＤパズルランド TOPへ