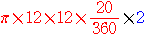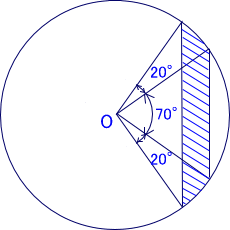

直線AC, BDに垂直な直線ODを引くと、∠AOC=∠OBD=55°であり、
三角形AOCと三角形OBDは3つの角が等しい同じ形の直角三角形である。
また、これら2つの直角三角形の斜辺(直角三角形で最も長い辺を斜辺という)
AOとOBは円の半径の長さであるから、長さが等しく、
結局、これら2つの直角三角形は形も面積も同じ三角形となる。
ここで、三角形EOCは、三角形AOCと三角形OBDが重なっている部分
であることに注意すると、それぞれの直角三角形から重なっている部分
を差し引いた残りの部分の面積は等しいので、三角形AOEと四角形ECDBの
面積は等しい。
従って、弧ABと直線AC, CD, DBとで囲まれた部分の面積は扇形AOBの
面積に等しい。
よって、求める面積は扇形AOBの面積の2倍である。
円周率をπ(πの値は約3.14です)とおくと、扇形AOBの面積は円の面積の
360分の20であるから、求める面積は下記の計算式で求められる。