答
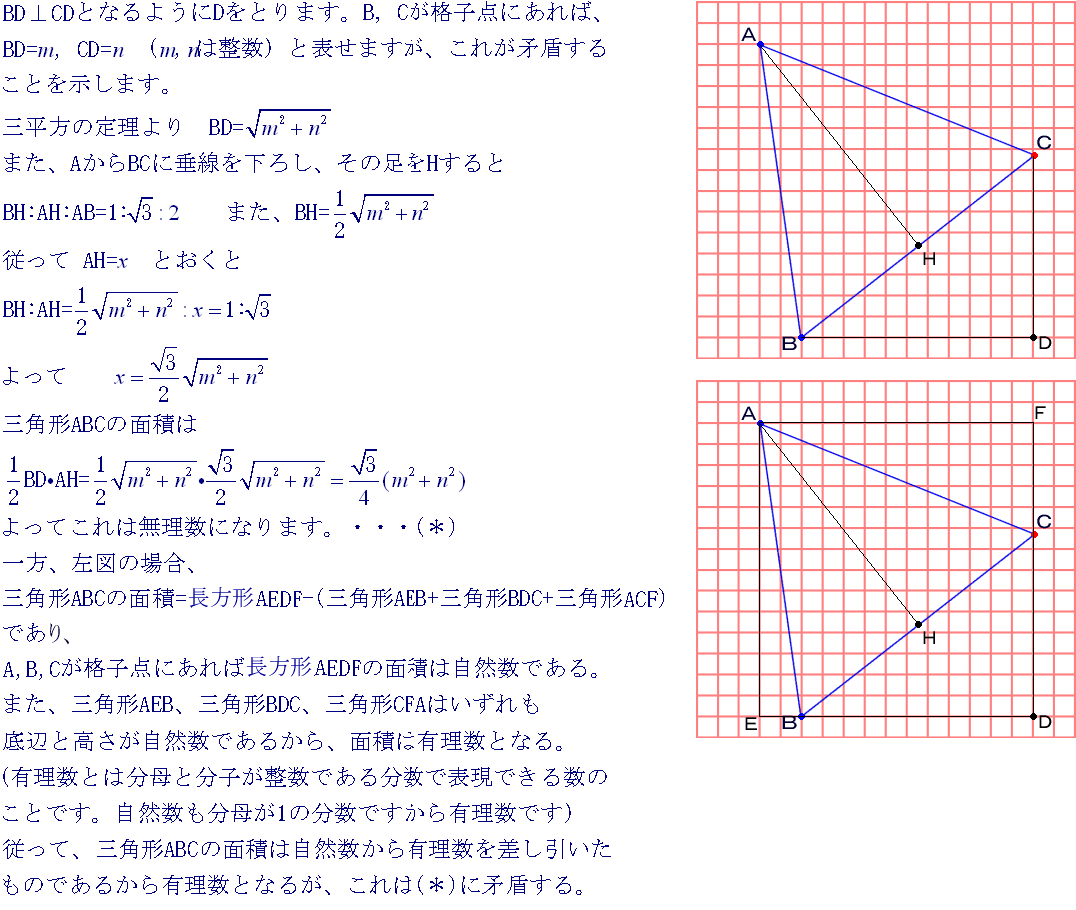
	Ａ，Ｂ，Ｃがどのような位置にあっても下記のように、そのうちの１点を頂点に、
	他の２点を辺の上に持ち、その辺が格子線と平行か垂直であるような、
	正三角形ＡＢＣに外接する長方形を描くことができる。
	このときＡ，Ｂ，Ｃが格子点にあれば、正三角形ＡＢＣの面積は下記に示すように
	無理数となるが、長方形の辺はいずれも格子線上にあるから、その面積は
	自然数×自然数となり、有理数である。（自然数も有理数のうちです）
	また、長方形の内部で正三角形以外の部分である直角三角形の面積も底辺と高さが
	自然数であるから有理数である。
	ここで、正三角形の面積は長方形から２個または３個の直角三角形を差し引いた
	ものであるが、（正三角形の１辺が格子線上にある場合は２個）これは、有理数か
	ら有理数を差し引いたものが無理数ということになり矛盾する。
	従って、３頂点を格子点にもつ正三角形は存在しない。
	※画像が表示されていない場合はしばらくお待ちください。
	※旧課程の高校数学には一次変換がありましたが、これを使って解くこともできます。
	ＩＭＤパズルランド　トップ