宇宙の亀　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　数学パズル
	※前回の串だんご�Vのオリジナルはニュートンがつくったパズルでしたが、
	今回のパズルはアインシュタインが出題しそうなパズルです。
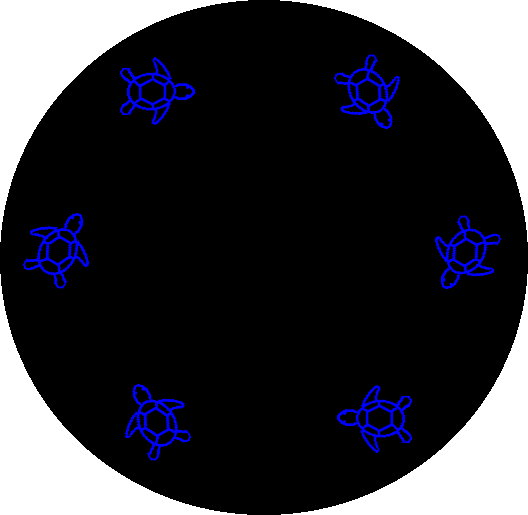
	下の図のように正六角形の頂点に亀がいて、それぞれ隣の亀に向かって
	進んでいきます。このとき頂点から隣の頂点までの距離は最初１ｋｍあり、
	同時刻における六匹の亀の速さは全て等しいものとします。六匹の亀は
	六角形の中心で出会うことになりますが、出発してから出会うまでの間に
	一匹の亀はどれだけ進むことになるでしょう。
	※図を書いていけばわかることですが、６匹の亀によって形作られる六角
	形は回転しながらだんだん小さくなっていき、亀はらせん状（渦巻き状）
	に進むことになります。
	※この問題は正方形の頂点に１匹ずつ計４匹の亀にした方がシンプルで
	パズルとしての傑作性がありますが、それだとちょっと図を書いただ
	けで勘で答えても当たってしまいそうですし、解法も、わかったよう
	なわかってないようなものが出てきそうですので上のように改作しま
	した。これだと本質的にわかっていないとやれないでしょう。
	●中学生には知識不足で解けないとは思いますが、ふつうの中学生でも
	説明すればわかるような簡単な解法がわかった方は、お知らせくださ
	い。
	※メールにはお名前と、おところを市、町、村、区まで入れてください。
	できましたらご職業(会社員、学生、高校生など)も入れてください。
	正解者一覧に掲載させて頂きます。
	●計算がほとんどいらない解法もありますが、これをアインシュタイン
	的解法と名付けておきます。
	このアインシュタイン的解法の背景には事象に対する通常の観念と
	は異なるものがあります。
	それは単に相対速度のことだけを意味しているわけではありません。
	重力が常に亀の甲羅に対して垂直に働くように亀が傾きながら旋回
	するとき、上に乗っている人にはどのような現象として観測される
	かを想像してみてください。
	●この種の問題は微分方程式や極座標などをつかって解くのが一般的
	であり、高校生には難しすぎると思いますが、高校数学の無限等比
	級数と極限の概念といった微積分の基本的な考え方をつかって割と
	簡単に解く方法（ニュートン式解法？）もあります。
	数学に自信のある方はその方法でも挑戦してみてください。
	ＩＭＤパズルランド 　トップページ